Stats/Methods I

Independent samples t-test

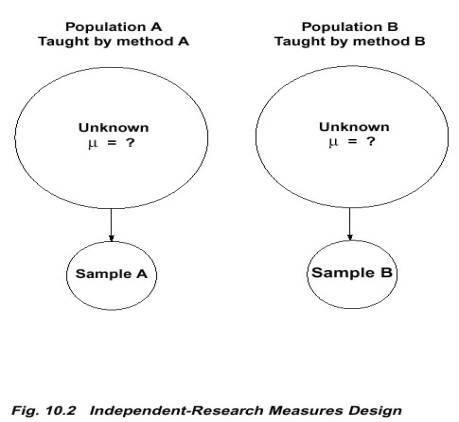
I. Independent Samples

Figure 10-3 (p. 314)
Two population distributions. The scores in population I vary from 50 to 70 (a 20-point spread)., and the scores in population II range from 20 to 30 (a 10-point spread). If you select one score from each of these two populations, the closest two values are X1 = 50 and X2 = 30. The two values that are farthest apart are X1 = 70 and X2 = 20.

A. Two Sources of Variability (error)

- each of the two samples will have some error as M represents m

- would be nice to simply add and then average the estimated standard errors from each sample

- can't (unless samples are the same size)

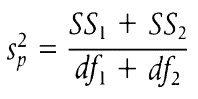
- Pooled Variance --allows the bigger sample to carry more weight in determining the final value

B. The formula

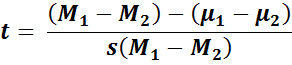
where:

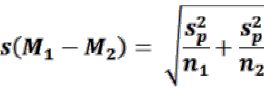
C. Degrees of Freedom

df = df1 + df2

= (n1 - 1) + (n2 - 1)

D. Assumptions

1. observations in each sample are independent

2. underlying populations are normal

3. the two populations being compared have equal variances (homogeneity of variance)

II. Single Sample vs. Two Independent Samples

A developmental psychologist would like to examine the difference in verbal skills for 10-year-old boys vs. 10-year-old girls. A sample of 10 boys and 10 girls is obtained and each child is given a standardized verbal abilities test. Do these data indicate a significant difference in verbal skills for boys compared to girls? Use two-tailed test and set alpha = .05.

Girls
M = 37
SS = 150
n = 10

Boys
M = 31
SS = 210
n = 10

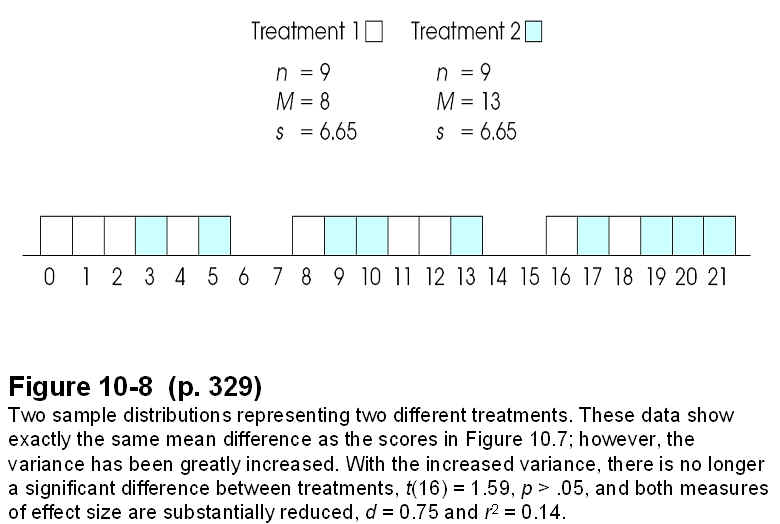
III. Variability and Effect Size